Confidence Interval For Population Variance

Confidence Intervals for Variance

In general, people tend to focus on the central tendency of a distribution, viewing variance merely as a stride in generating an error term for the mean. In some cases, however, the variance will exist the parameter of interest (information technology certainly was for Darwin), and so it is useful to know how to calculate confidence intervals for estimates of population variance.

Let us consider over again the formula for calculating a standardized deviate:

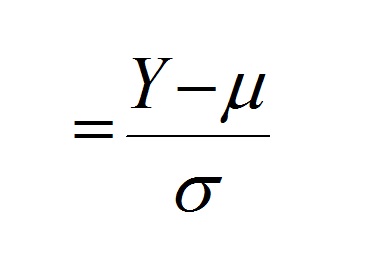
If we draw samples from a normal distribution, with a sample size of north, convert these observations to standardized normal deviates using the above formula, foursquare the standardized normal deviates, and take their sum:

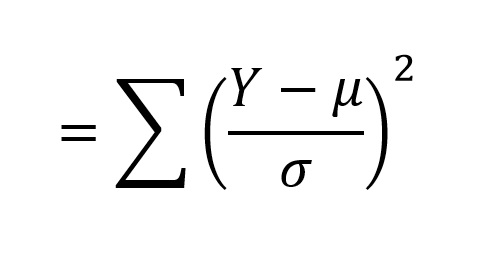
The distribution of these sums forms a probability distribution that should be familiar to y'all (at least by proper name): the χ²-distribution (Chi-square). Like the t-distribution, the shape of the χ²- distribution varies with the degrees of freedom (n - one in our case, where northward is the number of observations making up the sample), as can be seen in the post-obit graphs:

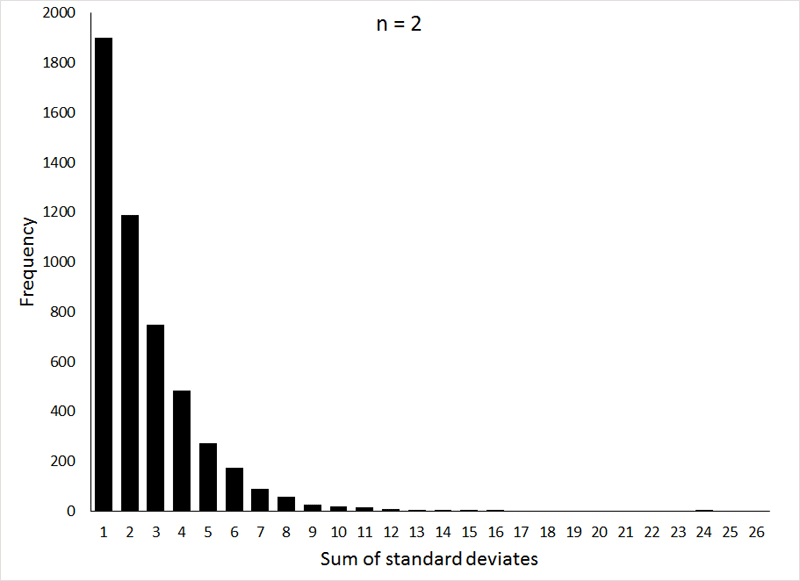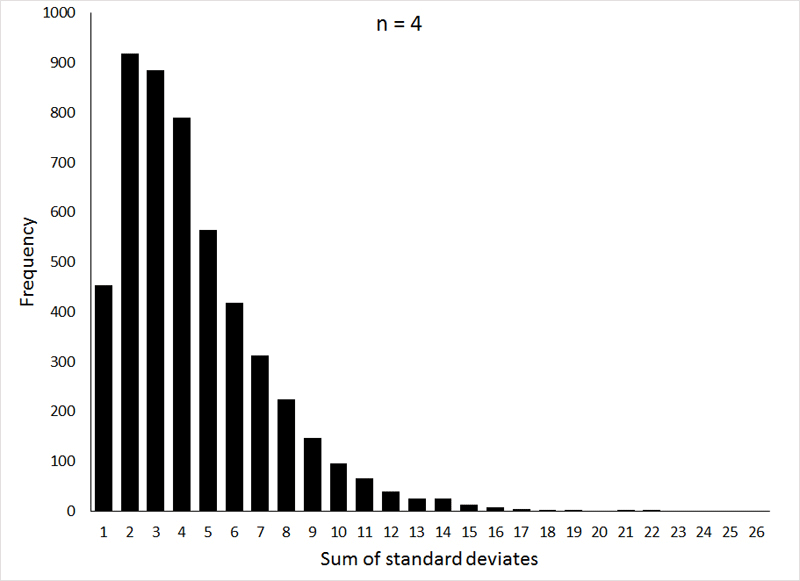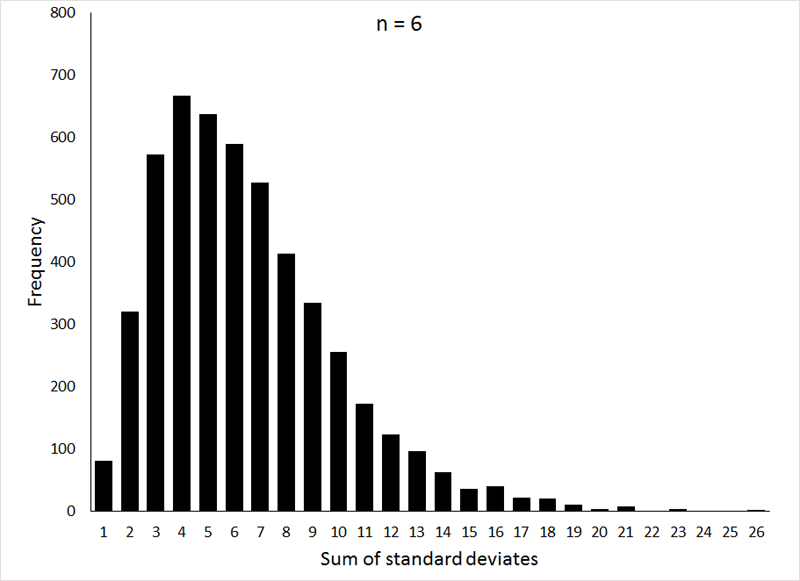
If the animation does not piece of work, or if you would like to see the individual graphs, they can be viewed Hither.

These graphs were generated (the R program can exist viewed HERE) by taking 5000 samples, with sample sizes of ii, 4, and half-dozen (corresponding to i, 3, and 5 degrees of liberty, respectively), from a normal distribution with μ = 0 and σ = 1, and squaring the sum of the observations.

Question 5: Await again at the formula for a standardized deviate, and explain why values drawn from a normal population where μ = 0 and σ = 1 tin exist considered as standardized normal deviates.

We can rewrite the formula for the variable shown in the distribution as:

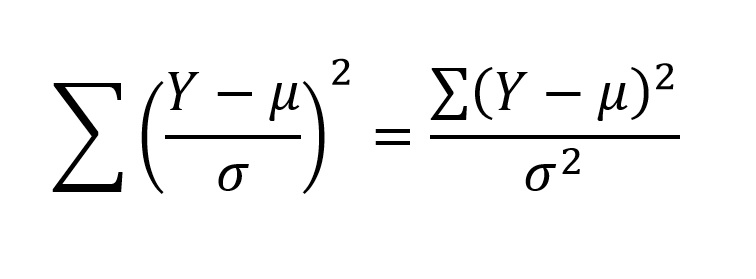
And employ it to sample data every bit shown below:

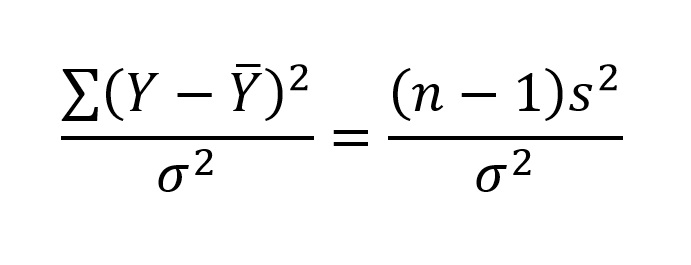
Note that the symbol for variance in the denominator has not inverse. This still is population variance. Knowing that these values follow a χ²-distribution means that we can decide the boundaries inside which 95% of the values volition occur. Because the χ^two-distribution is non symmetrical, we need to calculate the upper and lower conviction intervals separately. Table B.1 in your appendix (starting on page 672 in the 5th edition) shows the critical values for the χ^two-distribution. Equally with the t-distribution table, the left column contains the values for degrees of freedom (v), and at that place is a row of probabilities across the meridian. Again, the asymmetry of the distribution means that we will consider each tail separately.

Given that we are interested in 95% confidence intervals (α=0.05), the probabilities that we demand are 0.975 = 1-(α/2), which defines the left boundary (97.5% of the values exceed this value), and 0.025 = α/2, which defines the right purlieus. The reason we are using α/2 is because the 0.05 probability is divided betwixt the two tails. Thus, nosotros tin define the 95% limits for (north - one)s²/σ² as:

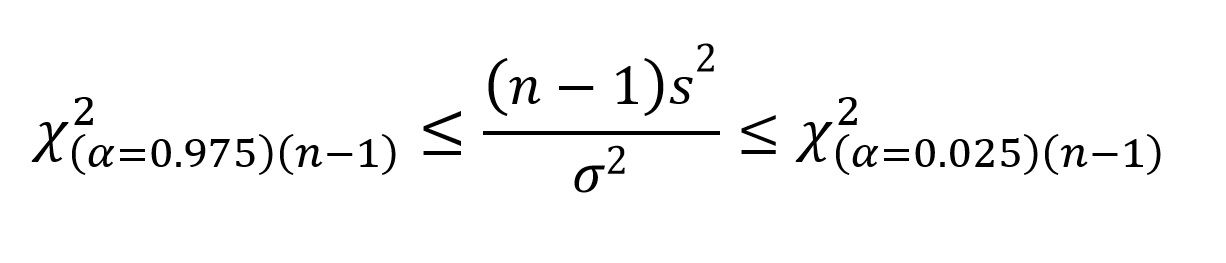
Where the χ² values are taken from the table. We can express this in terms of population variance (σ^two) as:

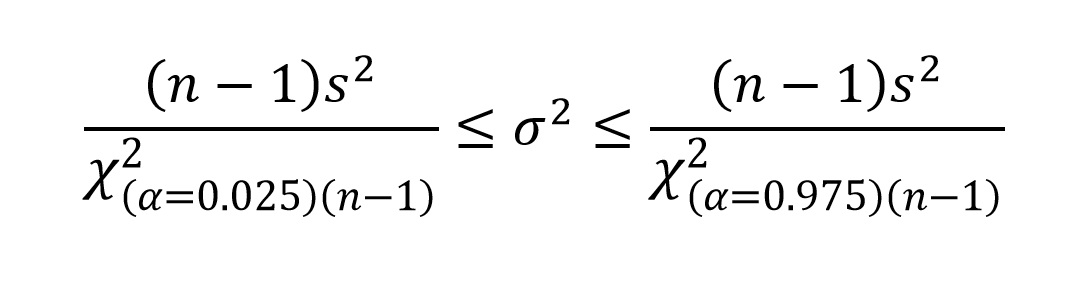
Remembering that sample variance (s²) is the sum of squares (∑y ²) divided by (n - 1), nosotros tin simplify (n - 1)s² as ∑y ²:

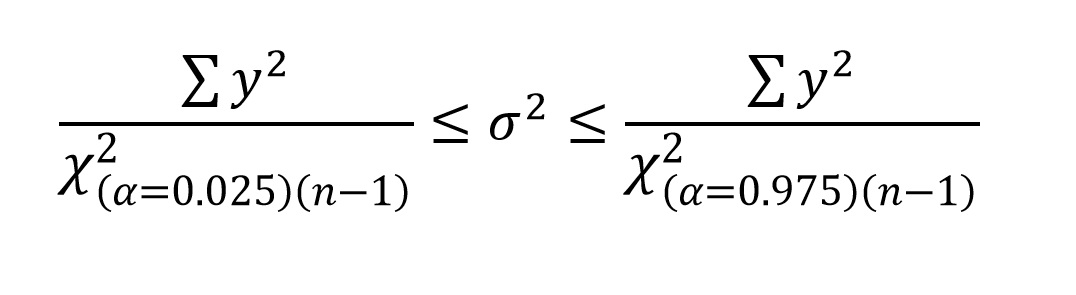
Provided that y'all think that ∑y ² is our annotation for the sum of squares (sum of the squared deviates), yous should have no problem calculating the 95% confidence intervals for an gauge of population variance (remember that sample variance is our approximate of population variance) using the above formula. Delight annotation that the value of α, and the degrees of liberty (n-1) are provided in the denominator as a subscript of χ². They are not office of the adding, they simply tell you lot where to detect the χ² value on the tabular array. Considering the conviction intervals are not symmetrical, they demand to exist reported in the same fashion shown in the formula, i.e., LCI ≤ σ² ≤ UCI.

Question 6: Calculate the sample variance, and the associated 95% conviction intervals for the variances for all 4 samples in your Excel workbook. Also, summate the 99% confidence intervals for the variance for the BAP data.

Conviction Intervals for Proportions

All likewise often, people will estimate a proportion (p = 10/n) from each of a series of samples, and then boilerplate these proportions across samples to produce a "mean proportion", and report south or SE of that mean as an estimate of the mistake in that proportion. This is wrong, for many reasons; of which we will address two. The starting time is that those measures of dispersion indicate the precision of the estimates (how like they are to one another), and not the accuracy (how close they are to the actual value) of the estimates. Second, it should be obvious that the proportion p = 0.75 estimated from a sample of 10000 is more likely to exist accurate than the same proportion estimated from a sample of four. Averaging estimated proportions beyond samples does not, in whatsoever way, take into account the sample sizes used to generate those estimates.

The solution is to pool the samples together into a unmarried sample, calculate the approximate of the proportion from that, and calculate 95% confidence intervals based on that sample. If you are interested in exploring this recommendation, or those that follow, in a little more depth, you can download THIS paper.

There are a number of options for calculating 95% confidence intervals for proportions, only I recommend using Wilson-score intervals, or Clopper-Pearson intervals (although the latter might be a little too bourgeois). Unfortunately, the calculation of either is cumbersome. Thus, I will provide you with a gift. You can download THIS spreadsheet, which does the calculations for you. For a proportion p = x/n, yous can input the values of ten and n, and both the Clopper-Pearson and Wilson score intervals will be calculated for you. Each interval is calculated every bit both the bodily proportion, and as the width, which is the number you would add (UCI) or decrease (LCI) from your proportion, p, to go the actual value. The latter is of keen use when presenting the 95% confidence intervals as error bars on a bar graph.

You are welcome.

Equally ever, salve your Word certificate and Excel spreadsheet as yourlastnameex5 and submit information technology to me via Blackboard.

Week five Objectives

Sympathize what constitutes a normal distribution

Understand how confidence intervals for a sample mean are derived from a distribution of sample means

Sympathise what the t-distribution represents

Sympathise what the "critical values" presented in statistical tables stand for, and how to identify them using degrees of freedom and alpha

Know how to generate conviction intervals from critical values

Transport comments, suggestions, and corrections to: Derek Zelmer